Задачи_огэ_высушенные_фрукты

Задачи огэ высушенные фрукты

Задание 21. Свежие фрукты содержат 72 % воды, а высушенные — 26 %. Сколько сухих фруктов получится из 222 кг свежих фруктов?

Так как в свежих фруктах содержится 72% воды, то сухого вещества в них 100-72=28%. Следовательно, масса сухого вещества в 222 кг фруктов, равна кг. После просушки, остается 26% воды, то есть 100-26=74% сухого вещества. Для вычисления массы сухих фруктов нужно разделить массу сухого вещества на, получим:

• Вариант 1
• Вариант 1. Задания по ОГЭ 2023. Математика. И.В. Ященко. 36 вариантов
• Решения заданий по номерам
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 25
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 25
  • 13
  • 13
  • 1-5
  • 1-5
  • 1-5
  • 25
  • 1-5
  • 25
  • 23
  • 23
  • 25
  • 25
  • Вариант 27
  • Задания 1-5 совпадают с Вариант 5. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Задания совпадают с Вариант 1. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
  • Кроме заданий:
    • 13
    • 14
    • 13
    • 14
    • 1-5
    • 8
    • 14
    • 24
    • 1-5
    • 8
    • 14
    • 1-5
    • 8
    • 14
    • 21
    • 22
    • 1-5
    • 8
    • 14
    • 21
    • 22
    • 23
    • 1
    • 8
    • 14
    • 25
    • 1
    • 8
    • 14
    • 25
    • 1
    • 14
    • 1
    • 14

    Частичное или полное копирование решений с данного сайта для распространения на других ресурсах,
    в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта

    Источник

    Задачи на процентное содержание ОГЭ №21

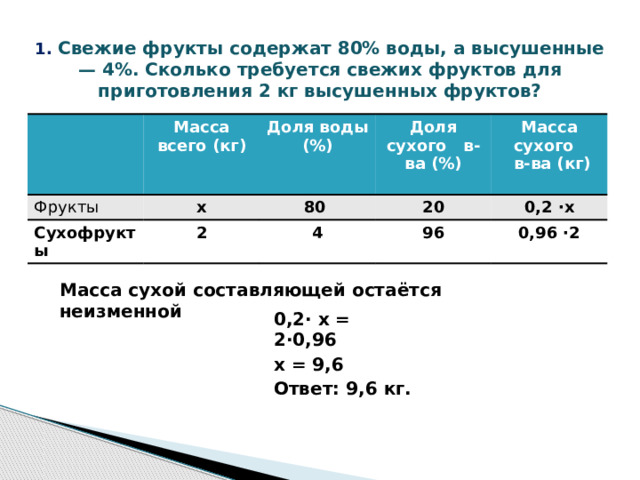
    Задачи с фруктами Надо знать: 1% = 0,01 Часть от числа находится умножением Масса сухой составляющей остаётся неизменной 1. Свежие фрукты содержат 80% воды, а высушенные — 4%. Сколько требуется свежих фруктов для приготовления 2 кг высушенных фруктов?

    1. Свежие фрукты содержат 80% воды, а высушенные — 4%. Сколько требуется свежих фруктов для приготовления 2 кг высушенных фруктов?

    Масса сухой составляющей остаётся неизменной

    Самостоятельная работа

    2.1 Свежие фрукты содержат 75% воды, а высушенные – 25%. Сколько требуется свежих фруктов для приготовления 45 кг высушенных фруктов?

    2.2 Свежие фрукты содержат 72% воды, а высушенные – 20%. Сколько сухих фруктов получится из 100 кг свежих фруктов?

    2.3 Сколько килограммов сухарей влажностью 25% можно получить из 225 кг хлеба влажностью 45%.

    Ответы: 1) 135 кг; 2) 35 кг; 3) 165 кг.

    Тренировочные упражнения

    Ответы: 4.1.105. 420 кг; 4.1.106. 90 кг.

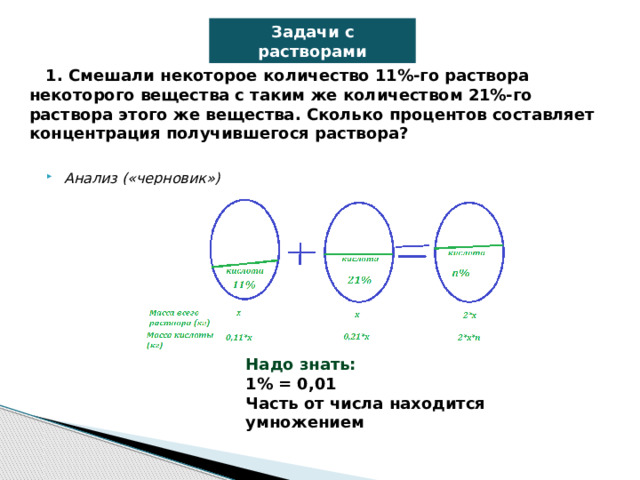
    1. Смешали некоторое количество 11%-го раствора некоторого вещества с таким же количеством 21%-го раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

    Надо знать: 1% = 0,01 Часть от числа находится умножением

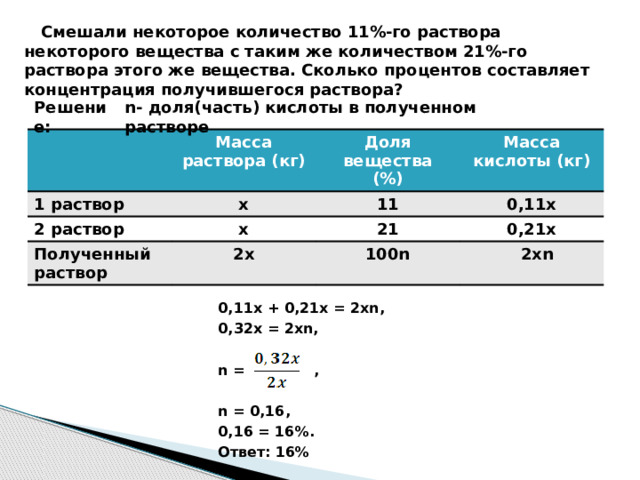
    Смешали некоторое количество 11%-го раствора некоторого вещества с таким же количеством 21%-го раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

    n- доля(часть) кислоты в полученном растворе

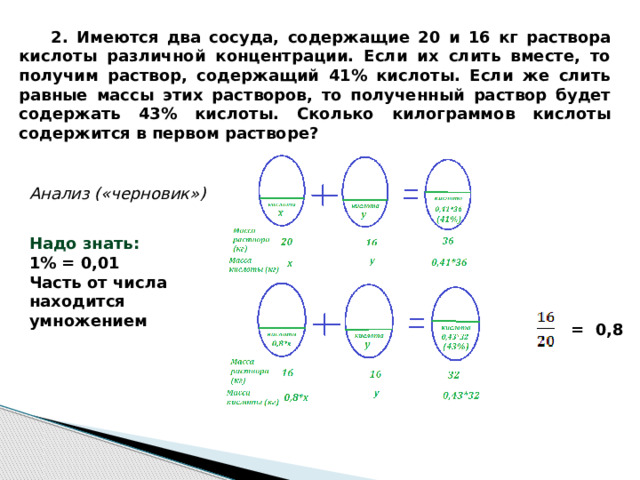
    2. Имеются два сосуда, содержащие 20 и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 41% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 43% кислоты. Сколько килограммов кислоты содержится в первом растворе?

    Надо знать: 1% = 0,01 Часть от числа находится умножением

    Имеются два сосуда, содержащие 20 и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 41% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 43% кислоты. Сколько килограммов кислоты содержится в первом растворе?

    Масса всего раствора (кг)

    Масса всего раствора (кг)

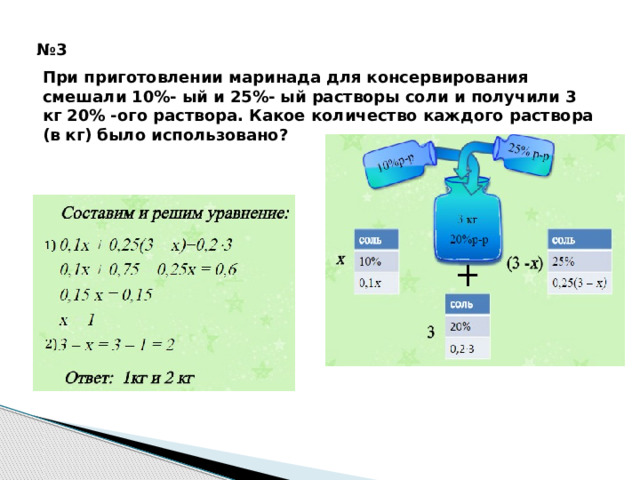
    При приготовлении маринада для консервирования смешали 10%- ый и 25%- ый растворы соли и получили 3 кг 20% -ого раствора. Какое количество каждого раствора (в кг) было использовано?

    Самостоятельная работа

    2.1. При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получился раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?

    2.2. Имеются два сосуда, содержащих 4 кг и 6 кг раствора кислоты разных концентраций. Если их слить вместе, то получится раствор, содержащий 35% кислоты. Если же слить равные массы этих растворов, то получится раствор, содержащий 36% кислоты. Сколько кг кислоты содержится в каждом сосуде?

    Ответы: 1) 2 : 1; 2) 1,64 кг, 1,86 кг.

    Тренировочные упражнения

    Ответы: 4.1.103. 2:1; 4.1.104. 2:1; 4.1.141. 15,6 кг; 4.1.142. 2,6 кг.

    • http://www.myshared.ru/slide/1100817/
    • http://matem-kovalenko.ucoz.ru/load/prezentacii_k_urokam/zadachi_na_procenty_zadanija_22_ogeh/2-1-0-7
    • http://www.uchportal.ru/video/vic/ogeh_gia_po_matematike/zadacha_22
    • http://dmou7.edumsko.ru/collective/pedagogical_collective/moskevich_larisa_vyacheslavovna/materials/materialy_k_uroku_matematiki/podgotovka_k_oge_zadacha_22/

    А. В. Семёнов, А. С. Трепалин, И. В. Ященко, П. И. Захаров, И. Р. Высоцкий. Математика . ФИПИ. Комплекс материалов для подготовки учащихся, ОГЭ 2016. Москва «Интеллект-Центр» 2016

    Источник

    ОГЭ, Математика.
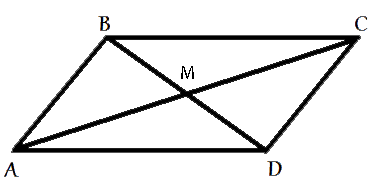
    Геометрия: Задача №56CD5D

    В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BMC.

    Решение задачи:

    Рассмотрим треугольники ABC и ACD.
    Сторона AC — общая для этих треугольников, AB=CD и BC=AD (по свойству параллелограмма), следовательно рассматриваемые треугольники равны (по третьему признаку). А значит равны и их площади, и равны эти площади половине площади параллелограмма.
    Рассмотрим треугольник ABC, как только что выяснили, площадь этого треугольника равна половине площади параллелограмма. Отрезок BM — является медианой (по третьему свойству параллелограмма), и соответственно делит этот треугольник на два равновеликих треугольника, т.е. равных по площади ( свойство медианы).
    Следовательно площадь BMC равна половине площади треугольника ABC. S BMC =S ABC /2=S ABCD /4.
    ч.т.д.

    Вы можете поблагодарить автора, написать свои претензии или предложения на странице ‘Про нас’

    Другие задачи из этого раздела

    Задача №890FB4

    Какие из данных утверждений верны? Запишите их номера.
    1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
    2) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
    3) Площадь круга меньше квадрата длины его диаметра.

    Задача №05C64C

    В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.

    Задача №FF0BCC

    Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.

    Задача №1EE527

    В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

    Задача №811D6E

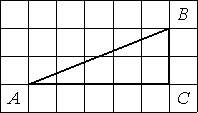
    Найдите тангенс угла В треугольника ABC, изображённого на рисунке.

    Источник

    Подготовка к ОГЭ по математике. Решение задачи 22. Задача о фруктах.

    Решите задачу: Свежие фрукты содержат 88% воды, а высушенные — 30%. Сколько сухих фруктов получится из 420 кг свежих фруктов?

    Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!

    	Поздравляем с Днём Знаний!
    	Примерный календарный план воспитательной работы на 2023-2024 учебный год
    	Совет Федерации одобрил закон об обязательном привлечении школьников к общественно полезному труду
    	Рособрнадзор сократит длительность всех ВПР до одного урока и постепенно переведёт их в компьютерную форму
    	В российских школах смогут работать учителя-предметники без высшего образования

    Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.

    © 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
    Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
    Территория распространения: Российская Федерация, зарубежные страны.
    Учредитель / главный редактор: Никитенко Е.И.

    Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
    Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
    При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
    Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

    Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

    Фотографии предоставлены

    Источник

    Читайте также:  Сушка_фруктов_промышленное_оборудование