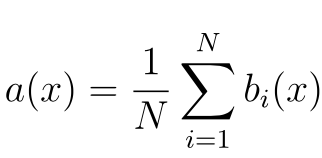Параметры_алгоритма_случайный_лес_random_forest

Случайный лес (Random Forest)

Случайный лес — один из самых потрясающих алгоритмов машинного обучения, придуманные Лео Брейманом и Адель Катлер ещё в прошлом веке. Он дошёл до нас в «первозданном виде» (никакие эвристики не смогли его существенно улучшить) и является одним из немногих универсальных алгоритмов. Универсальность заключается, во-первых, в том, что он хорош во многих задачах (по моим оценкам, 70% из встречающихся на практике, если не учитывать задачи с изображениями), во-вторых, в том, что есть случайные леса для решения задач классификации, регрессии, кластеризации, поиска аномалий, селекции признаков и т.д.

Этот пост — краткое практическое руководство для новичков — путеводитель по основным параметрам алгоритма с картинками (которые, кстати, построены на данных последнего конкурса Сбербанка и одной модельной задачи). Под тестом здесь понимается результат на скользящем контроле (для построения графиков использовано 5 фолдов), хотя для отложенного контроля (hold out) выводы будут такими же. Графики лежат в коридорах: дисперсионном и (если есть второй коридор) макс-минном. Все выводы и рекомендации — общие — не для конкретной задачи.

RF (random forest) — это множество решающих деревьев. В задаче регрессии их ответы усредняются, в задаче классификации принимается решение голосованием по большинству. Все деревья строятся независимо по следующей схеме:

• Выбирается подвыборка обучающей выборки размера samplesize (м.б. с возвращением) – по ней строится дерево (для каждого дерева — своя подвыборка).
• Для построения каждого расщепления в дереве просматриваем max_features случайных признаков (для каждого нового расщепления — свои случайные признаки).
• Выбираем наилучшие признак и расщепление по нему (по заранее заданному критерию). Дерево строится, как правило, до исчерпания выборки (пока в листьях не останутся представители только одного класса), но в современных реализациях есть параметры, которые ограничивают высоту дерева, число объектов в листьях и число объектов в подвыборке, при котором проводится расщепление.

Понятно, что такая схема построения соответствует главному принципу ансамблирования (построению алгоритма машинного обучения на базе нескольких, в данном случае решающих деревьев): базовые алгоритмы должны быть хорошими и разнообразными (поэтому каждое дерево строится на своей обучающей выборке и при выборе расщеплений есть элемент случайности).

В библиотеке scikit-learn есть такая реализация RF (привожу только для задачи классификации):

class sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion='gini', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features='auto', max_leaf_nodes=None, min_impurity_split=1e-07, bootstrap=True, oob_score=False, n_jobs=1, random_state=None, verbose=0, warm_start=False, class_weight=None)

С алгоритмом работают по стандартной схеме, принятой в scikit-learn:

from sklearn.ensemble import RandomForestRegressor from sklearn.metrics import roc_auc_score # далее - (X, y) - обучение, (X2, y2) - контроль # модель - здесь (для контраста) рассмотрим регрессор model = RandomForestRegressor(n_estimators=10 , oob_score=True, random_state=1) model.fit(X, y) # обучение a = model.predict(X2) # предсказание print ("AUC-ROC (oob) = ", roc_auc_score(y, model.oob_prediction_)) print ("AUC-ROC (test) = ", roc_auc_score(y2, a))

Опишем, что означают основные параметры:

Число деревьев — n_estimators

Чем больше деревьев, тем лучше качество, но время настройки и работы RF также пропорционально увеличиваются. Обратите внимание, что часто при увеличении n_estimators качество на обучающей выборке повышается (может даже доходить до 100%), а качество на тесте выходит на асимптоту (можно прикинуть, скольких деревьев Вам достаточно).

Источник

Параметры алгоритма случайный лес random forest

Здесь мы на основе классификации просто добавляем метод для отбора признаков.

Порядок действий в алгоритме

• Загрузите ваши данные.

• В заданном наборе данных определите случайную выборку.

• Далее алгоритм построит по выборке дерево решений.

• Дерево строится, пока в каждом листе не более n объектов, или пока не будет достигнута определенная высота.

• Затем будет получен результат прогнозирования из каждого дерева решений.

• На этом этапе голосование будет проводиться для каждого прогнозируемого результата: мы выбираем лучший признак, делаем разбиение в дереве по нему и повторяем этот пункт до исчерпания выборки.

• В конце выбирается результат прогноза с наибольшим количеством голосов. Это и есть окончательный результат прогнозирования.

Теоретическая составляющая алгоритма случайного дерева

По сравнению с другими методами машинного обучения, теоретическая часть алгоритма Random Forest проста. У нас нет большого объема теории, необходима только формула итогового классификатора a(x) :

• N – количество деревьев;
• i – счетчик для деревьев;
• b – решающее дерево;
• x – сгенерированная нами на основе данных выборка.

Стоит также отметить, что для задачи классификации мы выбираем решение голосованием по большинству, а в задаче регрессии – средним.

Реализация алгоритма Random Forest

Реализуем алгоритм на простом примере для задачи классификации, используя библиотеку scikit-learn:

• Имеет высокую точность предсказания, которая сравнима с результатами градиентного бустинга.

• Не требует тщательной настройки параметров, хорошо работает из коробки.

• Практически не чувствителен к выбросам в данных из-за случайного семплирования (random sample).

• Не чувствителен к масштабированию и к другим монотонным преобразованиям значений признаков.

• Редко переобучается. На практике добавление деревьев только улучшает композицию.

• В случае наличия проблемы переобучения, она преодолевается путем усреднения или объединения результатов различных деревьев решений.

• Способен эффективно обрабатывать данные с большим числом признаков и классов.

• Хорошо работает с пропущенными данными – сохраняет хорошую точность даже при их наличии.

• Одинаково хорошо обрабатывает как непрерывные, так и дискретные признаки

• Высокая параллелизуемость и масштабируемость.

Недостатки алгоритма

• Для реализации алгоритма случайного дерева требуется значительный объем вычислительных ресурсов.

• Большой размер моделей.

• Построение случайного леса отнимает больше времени, чем деревья решений или линейные алгоритмы.

• Алгоритм склонен к переобучению на зашумленных данных.

• Нет формальных выводов, таких как p-values, которые используются для оценки важности переменных.

• В отличие от более простых алгоритмов, результаты случайного леса сложнее интерпретировать.

• Когда в выборке очень много разреженных признаков, таких как тексты или наборы слов (bag of words), алгоритм работает хуже чем линейные методы.

• В отличие от линейной регрессии, Random Forest не обладает возможностью экстраполяции. Это можно считать и плюсом, так как в случае выбросов не будет экстремальных значений.

• Если данные содержат группы признаков с корреляцией, которые имеют схожую значимость для меток, то предпочтение отдается небольшим группам перед большими, что ведет к недообучению.

• Процесс прогнозирования с использованием случайных лесов очень трудоемкий по сравнению с другими алгоритмами.

Заключение

Метод случайного дерева (Random Forest) – это универсальный алгоритм машинного обучения с учителем. Его можно использовать во множестве задач, но в основном он применяется в проблемах классификации и регрессии.

Действенный и простой в понимании, алгоритм имеет значительный недостаток – заметное замедление работы при определенной настройке параметров внутри него.

Вы можете использовать случайный лес, если вам нужны чрезвычайно точные результаты или у вас есть огромный объем данных для обработки, и вам нужен достаточно сильный алгоритм, который позволит вам эффективно обработать все данные.

Дополнительные материалы:

Источник