Градиентный_бустинг_случайный_лес

Battle of the Ensemble — Random Forest vs Gradient Boosting

Two of the most popular algorithms in the world of machine learning, who will win?

If you have spent some time in the world of machine learning, you would have undoubtedly heard of a concept called the bias-variance tradeoff. It is one of the most important concepts any machine learning practitioner should learn and be aware of.

Essentially, the bias-variance tradeoff is a conundrum in machine learning which states that models with low bias will usually have high variance and vice versa.

Bias is the difference between the actual value and the expected value predicted by the model. A model with a high bias is said to be oversimplified as a result, underfitting the data.

Variance, on the other hand, represents a model’s sensitivity to small fluctuations in the training data. A model with high variance is sensitive to noise and as a result, overfitting the data. In other words, the model fits well on training data but fails to generalise on unseen (testing) data.

With that in mind, in this article, I would like to share one of several techniques to balance the tradeoff between bias and variance: ensemble methods.

First of all, what are ensemble methods?

Ensemble methods involve aggregating multiple machine learning models with the aim of decreasing both bias and variance. Ideally, the result from an ensemble method will be better than any of individual machine learning model.

There are 3 main types of ensemble methods:

For the purpose of this article, we will only focus on the first two: bagging and boosting. Specifically, we will examine and contrast two machine learning models: random forest and gradient boosting, which utilises the technique of bagging and boosting respectively.

Furthermore, we will proceed to apply these two algorithms in the second half of this article to solve the Titanic survival prediction competition in order to see how they work in practice.

Источник

Введение в машинное обучение

Один из общих подходов в машинном обучении заключается в использовании композиции «слабых» решающих правил. Итоговое правило строится путем взвешенного голосования ансамбля базовых правил. Для построения базовых правил и вычисления весов в последнее время часто используются две идеи:

• Баггинг (bagging – bootstrap aggregation): обучение базовых правил происходит на различных случайных подвыборках данных или/и на различных случайных частях признакового описания; при этом базовые правила строятся независимо друг от друга.
• Бустинг (boosting): каждое следующее базовое правило строится с использованием информации об ошибках предыдущих правил, а именно, веса объектов обучающей выборки подстраиваются таким образом, чтобы новое правило точнее работало на тех объектах, на которых предыдущие правила чаще ошибались.

Эксперименты показывают, что, как правило, бустинг работает на больших обучающих выборках, тогда как баггинг – на малых.

Одной из реализаций идеи баггинга является случайный лес [ 2 ].

Случайный лес, а точнее – случайные леса (random forests), является одним из наиболее универсальных и эффективных алгоритмов обучения с учителем, применимым как для задач классификации, так и для задач восстановления регрессии. Идея метода [ 2 ] заключается в использовании ансамбля из деревьев решений (например, ), которые обучаются независимо друг от друга. Итоговое решающее правило заключается в голосовании всех деревьев, входящих в состав ансамбля.

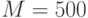
Для построения каждого дерева решений используется следующая процедура:

• Генерация случайной подвыборки из обучающей выборки путем процедуры изъятия с возвращением (так называемая бутстрэп-выборка). Размер данной подвыборки обычно составляет 50–70% от размера всей обучающей выборки.
• Построение дерева решений по данной подвыборке, причем в каждом новом узле дерева переменная для разбиения выбирается не из всех признаков, а из случайно выбранного их подмножества небольшой мощности . Дерево строится до тех пор, пока не будет достигнут минимальный размер листа 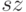(количество объектов, попавших в него). Рекомендуемые значения: для задачи классификации 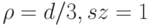, для задачи восстановления регрессии